Реализация алгоритмов Брезенхема

Сложно сегодня найти человека, который бы не сталкивался с машинной графикой в тех или иных проявлениях. Если человек начинает интересоваться алгоритмами, лежащими в её основе, то одними из первых будут алгоритмы Брезенхема. Беда лишь в том, что мне до сих пор не попадалось простого и вразумительного описания этих алгоритмов, а уж тем более — реализации. В этой статье я попытаюсь по возможности просто рассказать о семействе алгоритмов Брезенхема, а также приведу готовый к использованию код на JavaScript, который практически не отличается от кода на C/C++. Код можно брать и использовать, предварительно написав автору благодарственное письмо.

Хотелось бы выразить свои глубокие и искренние чувства к разработчикам стандартов www и тем, кто их реализует. Вариант JavaScript-кода, работающий во всех доступных броузерах, т.е. IE 6.0, NN 7.0 и Opera 6.0x, не отличается красотой и изысканностью. Впрочем, «к науке, которую я в настоящий момент представляю, это отношения не имеет».

Итак, назначение алгоритмов Брезенхема — нарисовать линию на растровом устройстве, как правило, на мониторе. Как можно видеть на рисунке 1, не все пиксели, входящие в изображение линии, лежат на этой линии, то есть задача алгоритма — найти наиболее близкие пиксели. Главное достоинство алгоритма Брезенхема в том, что в нём не используется в цикле дорогостоящая операция умножения. Алгоритм подходит для прямых или кривых второго порядка*. Существуют модификации алгоритма для четырёхсвязной (т.е. соседними считаются точки, отличающиеся на 1 по одной координате) и восьмисвязной (т.е. соседними считаются точки, обе координаты которых отличаются не больше, чем на 1) линий. Здесь приведён второй вариант — более сложный, но и дающий лучший результат.

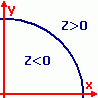Основная идея алгоритма в том, что линия, которую надо нарисовать, делит плоскость на две части. Уравнение кривой записывается в виде Z = f (x,y). Во всех точках кривой Z = 0, в точках, лежащих над кривой Z > 0, а в точках под кривой Z < 0. Нам известны координаты начала отрезка, то есть точки, заведомо лежащей на искомой кривой. Ставим туда первый пиксель и принимаем Z = 0. От текущего пикселя можно сделать два шага — либо по вертикали (по горизонтали), либо по диагонали на один пиксель. Конкретные направления шагов выбираются в зависимости от типа линии, которую надо нарисовать. Делая шаг, мы мы вычисляем, как изменятся значение Z:

ΔZ = Z'_xΔx + Z'_yΔy

При одном из возможных шагов Z растёт, при другом — уменьшается. Каждый шаг выбирается с тем расчётом, чтобы значение Z для нового пикселя было как можно ближе к 0. Таким образом, мы будем двигаться вдоль линии, создавая её изображение.

Рисование отрезка

Сразу договоримся, что алгоритм для прямой не рисует горизонтальные и вертикальные линии. Это связано с тем, что рисование таких линий можно реализовать гораздо более простым способом, часто на уровне BIOS или драйвера.

Оставшиеся отрезки делятся на две группы: горизонтальные и вертикальные. Если представить уравнение прямой в виде y = kx, то горизонтальными считаются отрезки, у которых |k| ≤ 1, а вертикальными — у которых |k| > 1. Отнеся отрезок к одной из групп, мы можем поменять местами координаты концов так, чтобы горизонтальные отрезки всегда рисовались слева направо, а вертикальные — сверху вниз.

Для горизонтальных отрезков каждый новый пиксель будет правее предыдущего на 1, при этом он может также быть выше (ниже), т.е. возможны два шага — вправо и вправо-по диагонали. Для вертикальных отрезков возможные шаги — вниз и вниз-по диагонали.

Если координаты концов отрезка (x₁,y₁) и (x₂,y₂) соответственно, то при каждом шаге по оси x Z изменяется на 1, а по оси y — на (x₂–x₁)/(y₂–y₁). Чтобы не связываться с делением и остаться в пределах целочисленной арифметики, переменную Z будем изменять соответственно на y2-y1 и x2-x1. Вот, собственно, и вся математика, остальное можно понять из кода.

Рисование окружности

Алгоритм рисования дуги останется за рамками статьи, а вот алгоритм для рисования окружности получился значительно проще, чем для прямой. Связано это со многими причинами.

Во-первых, мы рисуем только одну восьмую часть окружности — от π/2 до π/4, причём в обратном направлении, то есть по часовой стрелке. Вся остальная окружность получается путём отражения этой части относительно центра окружности, горизонтальной и вертикальной осей, а также прямых y = x + b и y = –x + b, проходящих через центр окружности.

Во-вторых из-за симметрии отклонения линии от окружности не так заметны, как отклонения от прямой, поэтому Z можно сравнивать с нулём, не вычисляя максимально допустимого отклонения.

Допустимые шаги — вправо и вправо-по диагонали, а изменение Z зависит от значений x и y, но зависимость линейная, поэтому операция умножения не требуется.

Вот, собственно, и всё. Ниже вы найдёте скрипт, демонстрирующий работу описанных алгоритмов, а для того, чтобы понять, как он работает, просто посмотрите исходный текст страницы.

Удачи!

3.04.2003